The grooves in a compact disc are very close together. One side of a disc can hold more music than two sides of a vinyl record.
Just how close are the grooves? We can use a laser to find out.
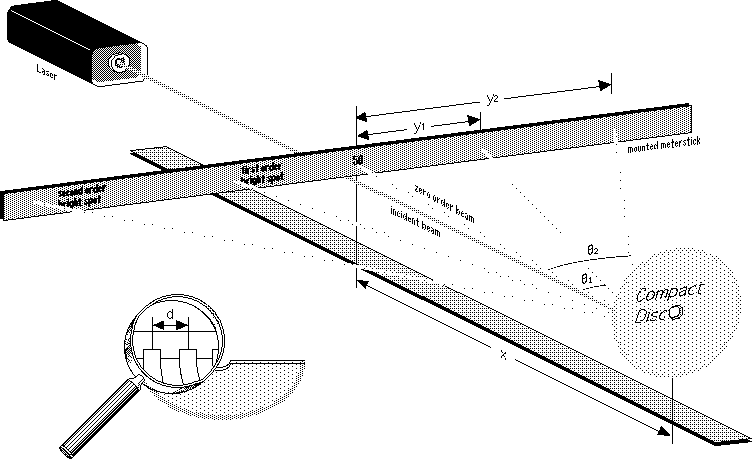
When a beam of light reflects from the "groovy" surface of a CD, a diffraction pattern is produced. To those who know how to analyze it, this pattern reveals the distance between the grooves. [A diagram of the arrangement is shown below.]
Fortunately, we know how to analyze the pattern.
The equation for the groove separation distance d may appear intimidating at first:
d = n(Lambda)/sin(Theta)
where n is the order of the bright spot in the pattern, Lambda is the wavelength of light reflecting from the CD to produce the diffraction pattern, and Theta is the angle of orientation of the bright spot. This angle is determined by measuring the distance x from the CD to the "screen" (in this case, the mounted meterstick) and the distance y of the first or second order bright spot from the central (zero order) bright spot.
A bit of clever trigonometry turns x and y into an angle Theta. Specifically,
Theta = Arctan(y/x)
The arctangent function is available on all scientific calculators.
So by knowing the wavelength of our laser light-632.8nm for the helium-neon laser we are using-and by measuring the distances x and y, we are able to determine the distance between the grooves on a compact disc.
What is that distance? Make the x and y measurements yourself and the demonstrator will be happy to carry out the calculations for you. [The actual distance of 1.6 micrometers is typically found to within one or two percent error.]